排序算法
概述
比较排序算法
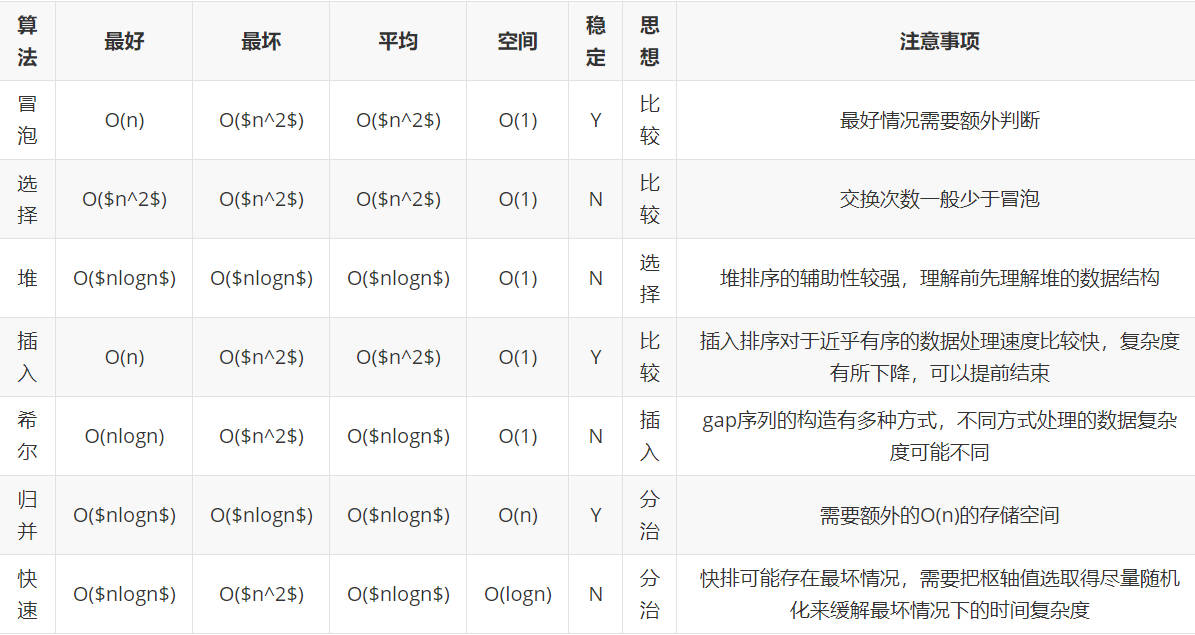
非比较排序算法
| 非比较排序算法 | 时间复杂度 | 空间复杂度 | 稳定性 |
|---|---|---|---|
| 计数排序 | O(n+k) | O(n+k) | 稳定 |
| 桶排序 | O(n+k) | O(n+k) | 稳定 |
| 基数排序 | O(d*(n+k)) | O(n+k) | 稳定 |
其中
- n 是数组长度
- k 是桶长度
- d 是基数位数
稳定 vs 不稳定
排序过程中会将排序前后值相同的元素的相对顺序打乱则为不稳定的排序,反之排序前后值相同的元素的相对顺序没有打乱则为稳定的排序
如:

Java 中的排序
Arrays.sort
JDK 7~13 中的排序实现
| 排序目标 | 条件 | 采用算法 |
|---|---|---|
| int[] long[] float[] double[] | size < 47 | 混合插入排序 (pair) |
| size < 286 | 双基准点快排 | |
| 有序度低 | 双基准点快排 | |
| 有序度高 | 归并排序 | |
| byte[] | size <= 29 | 插入排序 |
| size > 29 | 计数排序 | |
| char[] short[] | size < 47 | 插入排序 |
| size < 286 | 双基准点快排 | |
| 有序度低 | 双基准点快排 | |
| 有序度高 | 归并排序 | |
| size > 3200 | 计数排序 | |
| Object[] | -Djava.util.Arrays.useLegacyMergeSort=true | 传统归并排序 |
| TimSort |
1.冒泡排序(BubbleSort)
思想:每次比较冒出更大的一个元素
要点
- 每轮冒泡不断地比较相邻的两个元素,如果它们是逆序的,则交换它们的位置
- 下一轮冒泡,可以调整未排序的右边界,减少不必要比较
代码实现:
public class Bubble {
//递归实现 j代表未排序区域的右边界
public static void bubbleSort(int[] nums,int j){
if(j==0){
return;
}
for (int i=0;i<j;i++){
if(nums[i]>nums[i+1]){
int temp = nums[i];
nums[i] = nums[i+1];
nums[i+1] = temp;
}
}
bubbleSort(nums,j-1);
}
//优化 用变量x来充当已排序的边界,如x未改变则说明左边已经排序了就不用继续递归排序了
public static void bubbleSort3(int[] nums,int j){
if(j==0){
return;
}
int x = 0;
for (int i=0;i<j;i++){
if(nums[i]>nums[i+1]){
int temp = nums[i];
nums[i] = nums[i+1];
nums[i+1] = temp;
x=i;
}
}
bubbleSort3(nums,x);
}
//循环实现
public static void bubbleSort2(int[] nums){
for (int j = nums.length-1;j>0;j--) {
for (int i=0;i<j;i++){
if(nums[i]>nums[i+1]){
int temp = nums[i];
nums[i] = nums[i+1];
nums[i+1] = temp;
}
}
}
}
// 循环优化版
public static void bubbleSort3(int[] nums){
int x = 0;//记录上一次排序发送交换的位置
int j = nums.length -1;
while(true){
for (int i = 0; i < j; i++) {
if(nums[i]>nums[i+1]){
int temp = nums[i];
nums[i] = nums[i+1];
nums[i+1] = temp;
x = i;
}
}
j = x;
if(j==0){
break;
}
}
}
}
2.选择排序
要点:每轮选择,找出最大(最小元素),并把他交换到合适的位置
选择排序流程演示
代码实现:
public class Optional {
public static void optionalSort(int[] nums){
for (int i = nums.length-1; i >0 ; i--) {
int maxIdx = i;
for (int j = 0; j < i; j++) {
if(nums[j] > nums[maxIdx]){
maxIdx = j;
}
}
if(maxIdx!=i){
swap(nums,maxIdx,i);
}
}
}
private static void swap(int[] nums, int i , int j){
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
//选择排序变体 j代表未排序部分
public static void sort(int[] nums,int j){
if(j== nums.length-1){
return;
}
int index = j;
for (int i = j; i < nums.length-1 ; i++) {
if(nums[i]>nums[i+1]){
index = i+1;
}
}
int temp = nums[j];
nums[j] = nums[index];
nums[index] = temp;
sort(nums,j+1);
}
}
3.插入排序
要点
- 将数组分为两部分 [0 .. low-1] [low .. a.length-1]
- 左边 [0 .. low-1] 是已排序部分
- 右边 [low .. a.length-1] 是未排序部分
- 每次从未排序区域取出 low 位置的元素, 插入到已排序区域
代码实现:
public class Insertion {
//插入排序, low代表未排序部分 (循环)
public static void insertionSort(int[] nums){
for (int low = 1; low < nums.length; low++) {
int temp = nums[low];
int i = low-1;//已排序区域
while (i>=0 && nums[i]>temp){
nums[i+1] = nums[i];
i--;
}
if(i!=low-1){
nums[i+1] = temp;
}
}
}
//插入排序, j代表未排序部分(递归)
public static void insertionSort1(int[] nums,int j){
if(j== nums.length){
return;
}
int temp = nums[j];
int i = j-1; //已排序区域的指针
while (i>=0 && nums[i]>temp){//没有找到插入位置
nums[i+1] = nums[i];//空出插入位置
i--;
}
nums[i+1] = temp;//找到插入位置
insertionSort1(nums,j+1);
}
}
4.堆排序
要点:
- 建立大顶堆
- 每次将堆顶元素(最大值)交换到末尾,调整堆顶元素,让它重新符合大顶堆特性
代码实现:
public class HeapSort {
private static void sort(int[] nums){
heapify(nums,nums.length);
for (int i = nums.length-1; i>0; i--) {
swap(nums,0,i);
down(nums,0,i);
}
}
//建堆
private static void heapify(int[] nums,int size){
for (int i = size / 2 - 1; i >=0 ; i--) { //最后一个叶子节点的父节点就是最后一个非叶子节点
down(nums,i,size);
}
}
//下潜
private static void down(int[] nums,int parent,int size){
while (true){
int left = 2*parent+1;
int right = left+1;
int max = parent;
if(left<size && nums[max]<nums[left]){
max = left;
}
if(right<size && nums[max]<nums[right]){
max = right;
}
if(parent==max){
break;
}
swap(nums,parent,max);
parent =max;
}
}
private static void swap(int[] nums,int i,int j){
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}
5.希尔排序
要点
- 简单的说,就是分组实现插入,每组元素间隙称为 gap
- 每轮排序后 gap 逐渐变小,直至 gap 为 1 完成排序
- 对插入排序的优化,让元素更快速地交换到最终位置
代码实现:
public class ShellSort {
public static void sort(int[] nums){
//gap(间隙的选择) nums.length/2
for (int gap = nums.length >> 1; gap >=1 ; gap = gap >> 1) {
for (int low = gap; low < nums.length ; low++) {
int temp = nums[low];
int i = low - gap;
while (i>=0 && nums[i]>temp){
nums[i+gap] = nums[i];
i-=gap;
}
if(i!=low-gap) nums[i+gap] = temp;
}
}
}
}
6.归并排序
思想:分而治之
要点:
- 分 - 每次从中间切一刀,处理的数据少一半
- 治 - 当数据仅剩一个时可以认为有序
- 合 - 两个有序的结果
代码实现:
private void sort(int[] nums){
int[] temp = new int[nums.length];
spilt(nums,0,nums.length-1,temp);
}
private void spilt(int[] nums,int left,int right,int[] temp){
if(left==right){
return;
}
int m = (left+right) >>> 1;
spilt(nums,left,m,temp);
spilt(nums,m+1,right,temp);
merge(nums,left,m,m+1,right,temp);
}
/**
*
* @param nums 原始数组
* @param i 第一个有序范围
* @param iEnd
* @param j 第二个有序范围
* @param jEnd
* @param temp 临时数组
*/
private void merge(int[] nums,int i,int iEnd,int j,int jEnd,int[] temp){
int k = i;
int left = i;
while (i<=iEnd&&j<=jEnd){
if(nums[i]<nums[j]){
temp[k] = nums[i];
i++;
}else{
temp[k] = nums[j];
j++;
}
k++;
}
if(i>iEnd){
System.arraycopy(nums,j,temp,k, jEnd -j+1);
}
if(j>jEnd){
System.arraycopy(nums,i,temp,k,iEnd-i+1);
}
System.arraycopy(temp,left,nums,left,jEnd-left+1);
}
归并加插入:在归并排序治的时候采用插入排序而不是等到只有一个元素再开始合并,因为插入排序再数据量小时(元素< 32)效率最高
private void spilt(int[] nums,int left,int right,int[] temp){
if(right-left<=32){
insertion(a1, left, right);
return;
}
int m = (left+right) >>> 1;
spilt(nums,left,m,temp);
spilt(nums,m+1,right,temp);
merge(nums,left,m,m+1,right,temp);
}
public void insertion(int[] nums){
for (int low = 1; low < nums.length; low++) {
int temp = nums[low];
int i = low-1;//已排序区域
while (i>=0 && nums[i]>temp){
nums[i+1] = nums[i];
i--;
}
if(i!=low-1){
nums[i+1] = temp;
}
}
7.快速排序
单边循环(lomuto分区)要点
- 选择最右侧元素作为基准点
- j 找比基准点小的,i 找比基准点大的,一旦找到,二者进行交换
- 交换时机:j 找到小的,且与 i 不相等
- i 找到 >= 基准点元素后,不应自增
- 最后基准点与 i 交换,i 即为基准点最终索引
public class QuickSortLomuto {
public static void sort(int[] a){
quick(a,0,a.length-1);
}
private static void quick(int[] a,int left,int right){
if(left>=right){
return;
}
int p = partition(a,left,right);//执行分区,返回值为基准点元素的索引
quick(a,left,p-1);
quick(a,p+1,right);
}
private static int partition(int[] a,int left,int right){
int pv = a[right];//lomuto分区将最右侧的值当作基准点
int j= left;//初始化j的值等于left,j 负责寻找小于基准点元素的值
int i = left;//初始化i的值等于left,i 负责找大于基准点元素的值
while (j<right){
if(a[j] < pv){//j找到小于基准点的元素,i没有找到比基准点大的元素
if(i!=j){
swap(a,i,j);
}
i++;
}
j++;
}
swap(a,i,right);
return i;
}
private static void swap(int[] a,int i,int j){
int temp = a[i];
a[i] = a[j];
a[j] = temp;
}
快排优化(处理重复值)
class QuickSortHandleDuplicate{
public void sort(int[] nums){
quick(nums,0,nums.length-1);
}
private void quick(int[] nums, int left, int right) {
if(left>=right){
return;
}
int p = partition(nums,left,right);
quick(nums,left,p-1);
quick(nums,p+1,right);
}
/*
循环内
i 从 left + 1 开始,从左向右找大的或相等的
j 从 right 开始,从右向左找小的或相等的
交换,i++ j--
循环外 j 和 基准点交换,j 即为分区位置
*/
private int partition(int[] nums, int left, int right) {
int idx = ThreadLocalRandom.current().nextInt(right-left+1)+left;//获取随机基准点
swap(nums,left,idx);
int pv = nums[left];//获取基准点元素
int i = left+1;
int j = right;
while (i<=j){ //因为一开始 i 就可能等于 j,因此外层循环需要加等于条件保证至少进入一次,让 j 能减到正确位置
//i从左向右找比基准点大的元素
while (i<=j && nums[i]<pv){ //内层 while 循环中 i <= j 的 = 也不能去掉,因为 i == j 时也要做一次与基准点的判断,好让 i 及 j 到达正确位置
i++;
}
//j从右向左找比基准点小的元素
while (i<=j && nums[j]>pv){
j--;
}
if(i<=j){ //i == j 时,也要做一次 i++ 和 j-- 使下次循环二者不等才能退出
swap(nums,i,j);
i++;
j--;
}
}
swap(nums,left,j);
return j;
}
private void swap(int[] nums, int i, int j) {
int t = nums[i];
nums[i] = nums[j];
nums[j] = t;
}

评论